Função trigonométrica
Em matemática, as funções trigonométricas são funções angulares, importantes no estudo dos triângulos e na modelação de fenómenos periódicos. Podem ser definidas como razões entre dois lados de um triângulo retângulo em função de um ângulo, ou, de forma mais geral, como razões de coordenadas de pontos no círculo unitário. Na análise matemática, estas funções recebem definições ainda mais gerais, na forma de séries infinitas ou como soluções para certas equações diferenciais. Neste último caso, as funções trigonométricas estão definidas não só para ângulos reais como também para ângulos complexos.Atualmente, existem seis funções trigonométricas básicas em uso, cada uma com a sua abreviatura notacional padrão conforme tabela abaixo. As inversas destas funções são chamadas de função de arco ou funções trigonométricas inversas. A nomenclatura é feita através do prefixo "arco-", ou seja, arco seno, arco co-seno, etc. Matematicamente, são designadas por "arcfunção", i.e., arcsen, arccos, etc.; a notação usando-se −1 como na notação da função inversa não é recomendada, pois causa confusão com o inverso multiplicativo, como em sen-1 e cos-1. O resultado da função inversa é o ângulo que corresponde ao parâmetro da função. Por exemplo:
 .
.- fonte: wikipedia
Razões
trigonométricas
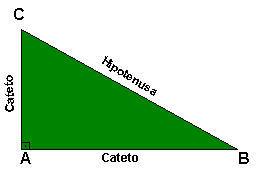
Catetos e Hipotenusa
Em um triângulo
chamamos o lado oposto ao ângulo reto de hipotenusa e os lados
adjacentes de catetos.Observe a figura:
 |
Hipotenusa: |
Seno, Cosseno e Tangente
Considere um triângulo retângulo BAC: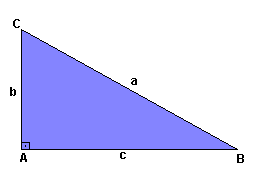 |
Hipotenusa: Ângulos: |
- Seno de um ângulo agudo é a razão entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa.
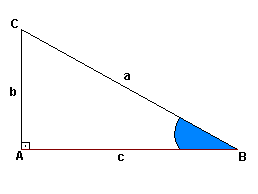 |
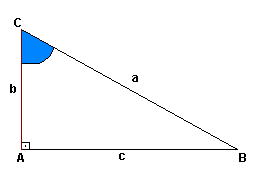 |
- Cosseno de um ângulo agudo é a razão entre a medida do cateto adjacente a esse ângulo e a medida da hipotenusa.
Assim:
 |

fonte: Só Matemática
|
Trigonometria: Seno, Cosseno e Tangente
Seno e cosseno
Dada
uma circunferência trigonométrica contendo o ponto A=(1,0) e um número
real x, existe sempre um arco orientado AM sobre esta circunferência,
cuja medida algébrica corresponde a x radianos. Seno: No plano cartesiano, consideremos uma circunferência trigonométrica, de centro em (0,0) e raio unitário. Seja M=(x',y') um ponto desta circunferência, localizado no primeiro quadrante, este ponto determina um arco AM que corresponde ao ângulo central a. A projeção ortogonal do ponto M sobre o eixo OX determina um ponto C=(x',0) e a projeção ortogonal do ponto M sobre o eixo OY determina outro ponto B=(0,y').
A medida do segmento OB coincide com a ordenada y' do ponto M e é definida como o seno do arco AM que corresponde ao ângulo a, denotado por sen(AM) ou sen(a).

sen(AM)=sen(a)=sen(a+2k )=y'
)=y'
 )=y'
)=y'Para simplificar os enunciados e definições seguintes, escreveremos sen(x) para denotar o seno do arco de medida x radianos.
Cosseno: O cosseno do arco AM correspondente ao ângulo a, denotado por cos(AM) ou cos(a), é a medida do segmento 0C, que coincide com a abscissa x' do ponto M.

cos(AM) = cos(a) = cos(a+2k ) = x'
) = x'
 ) = x'
) = x'
Tangente
Seja
a reta t tangente à circunferência trigonométrica no ponto A=(1,0). Tal
reta é perpendicular ao eixo OX. A reta que passa pelo ponto M e pelo
centro da circunferência intersecta a reta tangente t no ponto T=(1,t').
A ordenada deste ponto T, é definida como a tangente do arco AM
correspondente ao ângulo a.
tan(AM) = tan(a) = tan(a+k ) = µ(AT) = t'
) = µ(AT) = t'
Podemos
escrever M=(cos(a),sen(a)) e T=(1,tan(a)), para cada ângulo a do
primeiro quadrante. O seno, o cosseno e a tangente de ângulos do
primeiro quadrante são todos positivos. ) = µ(AT) = t'
) = µ(AT) = t'Um caso particular importante é quando o ponto M está sobre o eixo horizontal OX. Neste caso:
cos(0)=1, sen(0)=0 e tan(0)=0
Ampliaremos estas noções para ângulos nos outros quadrantes
Ângulos no segundo quadrante
Se
na circunferência trigonométrica, tomamos o ponto M no segundo
quadrante, então o ângulo a entre o eixo OX e o segmento OM pertence ao
intervalo  /2<a<
/2<a< .
Do mesmo modo que no primeiro quadrante, o cosseno está relacionado com
a abscissa do ponto M e o seno com a ordenada deste ponto. Como o ponto
M=(x,y) possui abscissa negativa e ordenada positiva, o sinal do seno
do ângulo a no segundo quadrante é positivo, o cosseno do ângulo a é
negativo e a tangente do ângulo a é negativa.
.
Do mesmo modo que no primeiro quadrante, o cosseno está relacionado com
a abscissa do ponto M e o seno com a ordenada deste ponto. Como o ponto
M=(x,y) possui abscissa negativa e ordenada positiva, o sinal do seno
do ângulo a no segundo quadrante é positivo, o cosseno do ângulo a é
negativo e a tangente do ângulo a é negativa.
cos( /2)=0 e sen(
/2)=0 e sen( /2)=1
/2)=1
A tangente não está definida, pois a reta OM não intercepta a reta t, pois elas são paralelas. /2)=0 e sen(
/2)=0 e sen( /2)=1
/2)=1
Ângulos no terceiro quadrante
O ponto M=(x,y) está localizado no terceiro quadrante, o que significa que o ângulo pertence ao intervalo:  <a<3
<a<3 /2.
Este ponto M=(x,y) é simétrico ao ponto M'=(-x,-y) do primeiro
quadrante, em relação à origem do sistema, indicando que tanto a sua
abscissa como a sua ordenada são negativos. O seno e o cosseno de um
ângulo no terceiro quadrante são negativos e a tangente é positiva.
/2.
Este ponto M=(x,y) é simétrico ao ponto M'=(-x,-y) do primeiro
quadrante, em relação à origem do sistema, indicando que tanto a sua
abscissa como a sua ordenada são negativos. O seno e o cosseno de um
ângulo no terceiro quadrante são negativos e a tangente é positiva.
 radianos, temos que
radianos, temos que
cos( )=-1, sen(
)=-1, sen( )=0 e tan(
)=0 e tan( )=0
)=0
 )=-1, sen(
)=-1, sen( )=0 e tan(
)=0 e tan( )=0
)=0
Ângulos no quarto quadrante
O ponto M está no quarto quadrante, 3 /2<a< 2
/2<a< 2 . O seno de ângulos no quarto quadrante é negativo, o cosseno é positivo e a tangente é negativa.
. O seno de ângulos no quarto quadrante é negativo, o cosseno é positivo e a tangente é negativa.
 /2, a tangente não está definida pois a reta OP não intercepta a reta t, estas são paralelas. Quando a=3
/2, a tangente não está definida pois a reta OP não intercepta a reta t, estas são paralelas. Quando a=3 /2, temos:
/2, temos:
cos(3 /2)=0, sin(3
/2)=0, sin(3 /2)=-1
/2)=-1
 /2)=0, sin(3
/2)=0, sin(3 /2)=-1
/2)=-1
Simetria em relação ao eixo OX
Em
uma circunferência trigonométrica, se M é um ponto no primeiro
quadrante e M' o simétrico de M em relação ao eixo OX, estes pontos M e
M' possuem a mesma abscissa e as ordenadas possuem sinais opostos.
sen(a) = -sen(b)
cos(a) = cos(b)
tan(a) = -tan(b)
cos(a) = cos(b)
tan(a) = -tan(b)
Simetria em relação ao eixo OY
Seja
M um ponto da circunferência trigonométrica localizado no primeiro
quadrante, e seja M' simétrico a M em relação ao eixo OY, estes pontos M
e M' possuem a mesma ordenada e as abscissa são simétricas.
sen(a) = sen(b)
cos(a) = -cos(b)
tan(a) = -tan(b)
cos(a) = -cos(b)
tan(a) = -tan(b)
Simetria em relação à origem
Seja
M um ponto da circunferência trigonométrica localizado no primeiro
quadrante, e seja M' simétrico de M em relação a origem, estes pontos M e
M' possuem ordenadas e abscissas simétricas.
sen(a) = -sen(b)
cos(a) = -cos(b)
tan(a) = tan(b)
cos(a) = -cos(b)
tan(a) = tan(b)
Senos e cossenos de alguns ângulos notáveis
Uma
maneira de obter o valor do seno e cosseno de alguns ângulos que
aparecem com muita frequência em exercícios e aplicações, sem
necessidade de memorização, é através de simples observação no círculo
trigonométrico.
Primeira relação fundamental
Uma
identidade fundamental na trigonometria, que realiza um papel muito
importante em todas as áreas da Matemática e também das aplicações é:
sin²(a) + cos²(a) = 1
que é verdadeira para todo ângulo a.Necessitaremos do conceito de distância entre dois pontos no plano cartesiano, que nada mais é do que a relação de Pitágoras. Sejam dois pontos, A=(x',y') e B=(x",y").


Se M é um ponto da circunferência trigonométrica, cujas coordenadas são indicadas por (cos(a),sen(a)) e a distância deste ponto até a origem (0,0) é igual a 1. Utilizando a fórmula da distância, aplicada a estes pontos, d(M,0)=[(cos(a)-0)²+(sen(a)-0)²]1/2, de onde segue que 1=cos²(a)+sin²(a).

Segunda relação fundamental
Outra relação fundamental na trigonometria, muitas vezes tomada como a definição da função tangente, é dada por:| tan(a) = | sen(a) cos(a) |
|---|
Se a=0, a=
 ou a=2
ou a=2 , temos que sen(a)=0, implicando que tan(a)=0, mas se a=
, temos que sen(a)=0, implicando que tan(a)=0, mas se a= /2 ou a=3
/2 ou a=3 /2,
segue que cos(a)=0 e a divisão acima não tem sentido, assim a relação
tan(a)=sen(a)/cos(a) não é verdadeira para estes últimos valores de a.
/2,
segue que cos(a)=0 e a divisão acima não tem sentido, assim a relação
tan(a)=sen(a)/cos(a) não é verdadeira para estes últimos valores de a.Para a
 0, a
0, a
 , a
, a 2
2 , a
, a
 /2 e a
/2 e a 3
3 /2, considere novamente a circunferência trigonométrica na figura seguinte.
/2, considere novamente a circunferência trigonométrica na figura seguinte.
| AT MN | = | OA ON |
|---|
 com a
com a
 /2 e a
/2 e a 3
3 /2 temos
/2 temos| tan(a) = | sen(a) cos(a) |
|---|
Forma polar dos números complexos
Um número complexo não nulo z=x+yi, pode ser representado pela sua forma polar:
z = r [cos(c) + i sen(c)]
onde r=|z|=R[x²+y²], i²=-1 e c é o argumento (ângulo formado entre o segmento Oz e o eixo OX) do número complexo z.
A = |A| [cos(a)+isen(a)]
B = |B| [cos(b)+isen(b)]
é dada pela Fórmula de De Moivre:B = |B| [cos(b)+isen(b)]
AB = |A||B| [cos(a+b)+isen(a+b)]
Isto
é, para multiplicar dois números complexos em suas formas
trigonométricas, devemos multiplicar os seus módulos e somar os seus
argumentos.Se os números complexos A e B são unitários então |A|=1 e |B|=1, e nesse caso
A = cos(a) + i sen(a)
B = cos(b) + i sen(b)
Multiplicando A e B, obtemosB = cos(b) + i sen(b)
AB = cos(a+b) + i sen(a+b)
Existe
uma importantíssima relação matemática, atribuída a Euler (lê-se
"óiler"), garantindo que para todo número complexo z e também para todo
número real z:
eiz = cos(z) + i sen(z)
Tal
relação, normalmente é demonstrada em um curso de Cálculo Diferencial,
e, ela permite uma outra forma para representar números complexos
unitários A e B, como:
A = eia = cos(a) + i sen(a)
B = eib = cos(b) + i sen(b)
onde a é o argumento de A e b é o argumento de B. Assim,B = eib = cos(b) + i sen(b)
ei(a+b) = cos(a+b)+isen(a+b)
Por outro lado
ei(a+b) = eia . eib = [cos(a)+isen(a)] [cos(b)+isen(b)]
e desse modo
ei(a+b) = cos(a)cos(b) - sen(a)sen(b)
+ i [cos(a)sen(b) + cos(b)sen(a)]
Para que dois números complexos sejam iguais, suas partes reais e imaginárias devem ser iguais, logo+ i [cos(a)sen(b) + cos(b)sen(a)]
cos(a+b) = cos(a)cos(b) - sen(a)sen(b)
sen(a+b) = cos(a)sen(b) + cos(b)sen(a)
Para a diferença de arcos, substituímos b por -b nas fórmulas da somasen(a+b) = cos(a)sen(b) + cos(b)sen(a)
cos(a+(-b)) = cos(a)cos(-b) - sen(a)sen(-b)
sen(a+(-b)) = cos(a)sen(-b) + cos(-b)sen(a)
para obtersen(a+(-b)) = cos(a)sen(-b) + cos(-b)sen(a)
cos(a-b) = cos(a)cos(b) + sen(a)sen(b)
sen(a-b) = cos(b)sen(a) - cos(a)sen(b)
sen(a-b) = cos(b)sen(a) - cos(a)sen(b)
Seno, cosseno e tangente da soma e da diferença
Na circunferência trigonométrica, sejam os ângulos a e b com 0£a£2 e 0£b£2
e 0£b£2 , a>b, então;
, a>b, então;
sen(a+b) = sen(a)cos(b) + cos(a)sen(b)
cos(a+b) = cos(a)cos(b) - sen(a)sen(b)
Dividindo a expressão de cima pela de baixo, obtemos:cos(a+b) = cos(a)cos(b) - sen(a)sen(b)
| tan(a+b)= | sen(a)cos(b)+cos(a)sen(b) cos(a)cos(b)-sen(a)sen(b) |
|---|
| tan(a+b)= | tan(a)+tan(b) 1-tan(a)tan(b) |
|---|
sen(a-b) = sen(a)cos(b) - cos(a)sen(b)
cos(a-b) = cos(a)cos(b) + sen(a)sen(b)
cos(a-b) = cos(a)cos(b) + sen(a)sen(b)
fonte: http://matematicadekelsio.blogspot.com.br/2009/09/trigonometria-seno-cosseno-e-tangente.html
TRIGONOMETRIA

| A onda
marítima mais alta registrada oficialmente foi medida a bordo do navio
norte-americano Ramapo, durante a noite de 6 de fevereiro de 1993.
Utilizando cálculos trigonométricos, o tenente Margraff pôde
averiguar que a onda tinha, até a sua crista, uma altura aproximada de
34 metros.
A
palavra trigonometria (do grego trigono=triangular e metria=medida) teve
origem na resolução de problemas práticos relacionados principalmente
à navegação e à Astronomia.
Acredita-se que, como
ciência, a Trigonometria nasceu com o astrônomo grego Hiparco de Nicéia
(190 a.C.-125 a.C.). Este grande astrônomo criou uma matemática
aplicada para prever os eclipses e os movimentos dos astros, permitindo
a elaboração de calendários mais precisos e maior segurança na
navegação. Hiparco ficou conhecido como pai da Trigonometria, por ter
estudado e sistematizado algumas relações entre os elementos de um triângulo.
A
trigonometria, que relaciona as medidas dos lados de um triângulo com
as medidas de seus ângulos, é de grande utilidade na medição de distâncias
inacessíveis ao ser humano, como a altura de montanhas, torres e árvores,
ou a largura de rios e lagos. Por esse motivo, a Trigonometria foi
considerada em sua origem, como uma extensão da Geometria.
Ela
não se limita ao estudo de triângulos. Encontramos aplicações da
Trigonometria na Engenharia, na Mecânica, na Eletricidade, na Acústica,
na Medicina, na Astronomia e até na Música.
Há
indícios de que os babilônicos (habitantes da antiga Mesopotâmia,
hoje Iraque) efetuaram estudos rudimentares de trigonometria.
Mais
tarde, a Astronomia, estudada por egípcios e gregos, foi a grande
impulsora do desenvolvimento da Trigonometria. |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Sistemas Lineares
Equação linear é toda equação da forma:
a1x1 + a2x2+
a3x3 + ... + anxn = b
em que a1, a2,
a3, ... , an são números reais, que recebem o nome de coeficientes
das incógnitas
x1, x2,x3,
... , xn, e b é um número real chamado termo independente (
quando b=0, a equação recebe o nome de linear homogênea).
Veja alguns exemplos de equações
lineares:
|
|
|
As equações a seguir não são lineares:
|
|
Sistema linear
Um conjunto de equações lineares da forma:
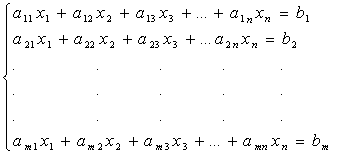
é um sistema linear de m equações e
n incógnitas.
A solução de um sistema linear é a n-upla de números reais ordenados (r1,
r2, r3,..., rn) que é, simultaneamente,
solução de todas as equações do sistema.
Matrizes associadas a um sistema linear
Matrizes associadas a um sistema linear
A um
sistema linear podemos associar as seguintes matrizes:
-
matriz incompleta: a matriz A formada pelos coeficientes das incógnitas do sistema.
Em relação ao sistema:
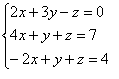
a matriz incompleta é:
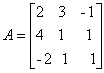
-
matriz completa: matriz B que se obtém acrescentando à matriz incompleta uma última coluna formada pelos termos independentes das equações do sitema.
Assim, para o mesmo sistema acima, a matriz
completa é:
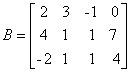
Sistemas homogêneos
Um sistema é
homogêneo quando todos os termos independentes da equações são nulos:
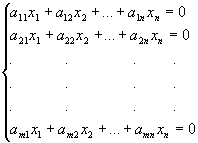
Veja um exemplo:
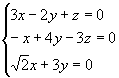
A n-upla (0, 0, 0,...,0) é sempre solução
de um sistema homogêneo com n incógnitas e recebe o nome de solução
trivial. Quando existem, as demais soluções são chamadas não-triviais.
Classificação de um sistema
quanto ao número de soluções
Resolvendo o sistema 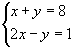 , encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o
sistema é possível (tem solução) e determinado (solução única).
, encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o
sistema é possível (tem solução) e determinado (solução única).
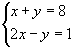 , encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o
sistema é possível (tem solução) e determinado (solução única).
, encontramos uma única solução: o par ordenado (3,5). Assim, dizemos que o
sistema é possível (tem solução) e determinado (solução única).
No caso do sistema 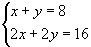 ,
verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são
algumas de suas infinitas soluções. Por isso, dizemos que o sistema é
possível (tem solução) e indeterminado (infinitas soluções).
,
verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são
algumas de suas infinitas soluções. Por isso, dizemos que o sistema é
possível (tem solução) e indeterminado (infinitas soluções).
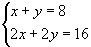 ,
verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são
algumas de suas infinitas soluções. Por isso, dizemos que o sistema é
possível (tem solução) e indeterminado (infinitas soluções).
,
verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são
algumas de suas infinitas soluções. Por isso, dizemos que o sistema é
possível (tem solução) e indeterminado (infinitas soluções).
Para 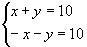 ,
verificamos que nenhum par ordenado satisfaz simultaneamente as equações.
Portanto, o sistema é impossível (não tem solução).
,
verificamos que nenhum par ordenado satisfaz simultaneamente as equações.
Portanto, o sistema é impossível (não tem solução).
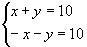 ,
verificamos que nenhum par ordenado satisfaz simultaneamente as equações.
Portanto, o sistema é impossível (não tem solução).
,
verificamos que nenhum par ordenado satisfaz simultaneamente as equações.
Portanto, o sistema é impossível (não tem solução).Resumindo, um sistema linear pode ser:
a) possível e determinado (solução única);
b) possível e indeterminado (infinitas soluções);
c) impossível (não tem solução).
b) possível e indeterminado (infinitas soluções);
c) impossível (não tem solução).
Sistema normal
Um sistema é normal
quando tem o mesmo número de equações (m) e de incógnitas (n)
e o determinante da matriz incompleta associada ao sistema é diferente de zero.
Se m=n e det A 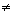 0,
então o sistema é normal.
0,
então o sistema é normal.
Regra de Cramer
Todo sistema normal tem uma
única solução dada por:
em que i 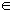 { 1,2,3,...,n}, D= det A é o determinante da matriz incompleta associada ao
sistema, e Dxi é o determinante obtido pela substituição, na
matriz incompleta, da coluna i pela coluna formada pelos termos
independentes.
{ 1,2,3,...,n}, D= det A é o determinante da matriz incompleta associada ao
sistema, e Dxi é o determinante obtido pela substituição, na
matriz incompleta, da coluna i pela coluna formada pelos termos
independentes.
Discussão de um sistema
linear
Se um sistema linear tem n
equações e n incógnitas, ele pode ser:
a) possível e
determinado,
se D=det A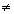 0; caso em
que a solução é única.
0; caso em
que a solução é única.
Exemplo:
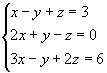
m=n=3
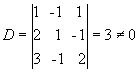
Então, o sistema é possível e determinado,
tendo solução única.
b) possível e
indeterminado, se D= Dx1 = Dx2 = Dx3 = ... = Dxn= 0,
para
n=2. Se n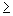 3, essa
condição só será válida se não houver equações com coeficientes das
incógnitas respectivamente proporcionais e termos independentes
não-proporcionais.
3, essa
condição só será válida se não houver equações com coeficientes das
incógnitas respectivamente proporcionais e termos independentes
não-proporcionais.
Um sistema possível e indeterminado
apresenta infinitas soluções.
Exemplo:
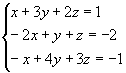
D=0, Dx =0, Dy=0 e Dz=0
Assim, o sistema é possível e
indeterminado, tendo infinitas soluções.
c) impossível, se D=0 e 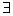 Dxi
Dxi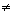 0, 1
0, 1 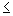 i
i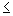 n;
caso
em que o sistema não tem solução.
n;
caso
em que o sistema não tem solução.
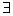 Dxi
Dxi
Exemplo:
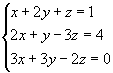
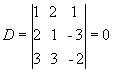
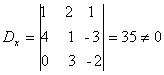
Como D=0 e Dx 0,
o sistema é impossível e não apresenta solução.
0,
o sistema é impossível e não apresenta solução.
Sistemas Equivalentes
Dois sistemas são
equivalentes quando possuem o mesmo conjunto solução.
Por exemplo, dados os
sistemas:
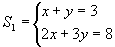 e
e 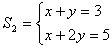
verificamos que o par ordenado (x, y) = (1,
2) satisfaz ambos e é único. Logo, S1 e S2 são
equivalentes: S1 ~ S2.
Propriedades
a) Trocando de posição as
equações de um sistema, obtemos outro sistema equivalente.
Por exemplo:
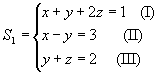 e
e 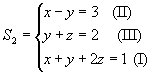
S1 ~S2
b) Multiplicando uma ou mais equações de um sistema por um número K (K

S1 ~S2
c) Adicionando a uma das equações de um
sistema o produto de outra equação desse mesmo sistema por um número k
( K 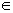 IR*), obtemos um
sistema equivalente ao anterior.
IR*), obtemos um
sistema equivalente ao anterior.
Por exemplo:
Dado 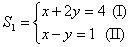 , substituindo a equação (II) pela soma do produto de (I) por -1 com (II),
obtemos:
, substituindo a equação (II) pela soma do produto de (I) por -1 com (II),
obtemos:
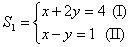 , substituindo a equação (II) pela soma do produto de (I) por -1 com (II),
obtemos:
, substituindo a equação (II) pela soma do produto de (I) por -1 com (II),
obtemos: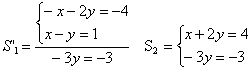
Sistemas escalonados
Utilizamos a regra de Cramer para discutir e resolver sistemas lineares em que o
número de equações (m) é igual ao número de incógnitas (n).
Quando m e n são maiores que três, torna-se muito trabalhoso
utilizar essa regra. Por isso, usamos a técnica do escalonamento, que
facilita a discussão e resolução de quaisquer sistemas lineares.
Dizemos que um sistema, em que existe pelo menos um coeficiente não-nulo em
cada equação, está escalonado se o número de coeficientes nulos antes do
primeiro coeficiente não nulo aumenta de equação para equação.
Para escalonar um sistema adotamos o seguinte procedimento:
a) Fixamos como 1º equação
uma das que possuem o coeficiente da 1º incógnita diferente de zero.
b) Utilizando as propriedades
de sistemas equivalentes, anulamos todos os coeficientes da 1ª incógnita das
demais equações.
c) Repetimos o processo com
as demais incógnitas, até que o sistema se torne escalonado.
Vamos então aplicar a técnica do escalonamento, considerando dois tipos de
sistema:
I. O número de equações é
igual ao número de incógnitas (m=n)
Exemplo 1:
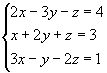
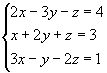
1ºpasso: Anulamos
todos os coeficientes da 1º incógnita a partir da 2º equação, aplicando as
propriedades dos sistemas equivalentes:
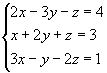 |
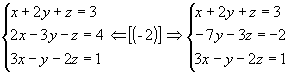 |
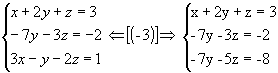 |
2º passo: Anulamos os
coeficientes da 2º incógnita a partir da 3º equação:
 |
Agora o sistema está escalonado e podemos
resolvê-lo.
-2z=-6 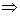 z=3
z=3
Substituindo z=3 em (II):
-7y - 3(3)= -2 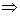 -7y - 9 = -2
-7y - 9 = -2 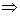 y=-1
y=-1
Substituindo z=3 e y=-1 em (I):
x + 2(-1) + 3= 3 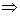 x=2
x=2
Então, x=2, y=-1 e z=3
Exemplo 2: 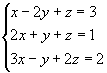
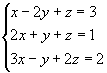
1º passo: Anulamos todos os
coeficientes da 1º incógnita a partir da 2º equação:
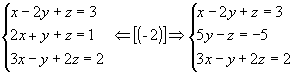 |
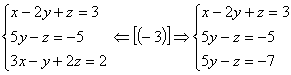 |
2º passo: Anulamos os coeficientes da
2ª incógnita, a partir da 3º equação:
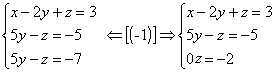 |
Dessa forma, o sistema está escalonando.
Como não existe valor real de z tal que 0z=-2, o sistema é impossível.
II) O número de equações é menor que o
número de incógnitas (m < n)
Exemplo: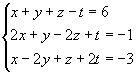
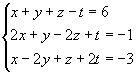
1º passo: Anulamos todos os
coeficientes da 1º incógnita a partir da 2º equação:
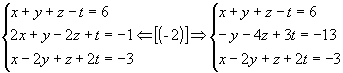 |
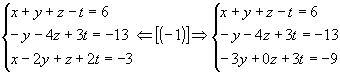
|
2º passo: Anulamos os coeficientes da
2º incógnita, a partir da 3º equação:
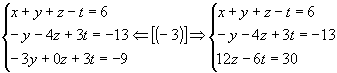 |
O sistema está escalonado. Como m<n, o
sistema é possível e indeterminado, admitindo infinitas soluções. A
diferença entre o número de incógnitas (n) e o de equações (m) de um
sistema nessas condições é chamada grau de indeterminação (GI):
GI= n - m
Para resolver um sistema indeterminado,
procedemos do seguinte modo:
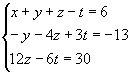 |
|
Como o grau de indeterminação é 1,
atribuímos a uma das incógnitas um valor 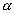 ,
supostamente conhecido, e resolvemos o sistema em função desse valor. Sendo t=
,
supostamente conhecido, e resolvemos o sistema em função desse valor. Sendo t=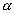 ,
substituindo esse valor na 3º equação, obtemos:
,
substituindo esse valor na 3º equação, obtemos:
12z - 6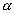 =
30
=
30 12z= 30 + 6
12z= 30 + 6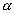
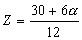 =
=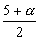
Conhecidos z e t, substituímos
esses valores na 2º equação:
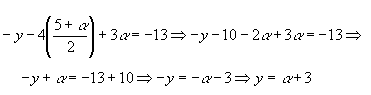
Conhecidos z,t e y,
substituímos esses valores na 1º equação:
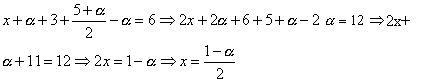
Assim, a solução do sistema é dada por S=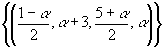 ,
com
,
com 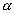
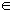 IR.
IR.
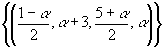 ,
com
,
com
Para cada valor que seja atribuído a 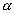 ,
encontraremos uma quádrupla que é solução para o sistema.
,
encontraremos uma quádrupla que é solução para o sistema.
Determinantes
Como já
vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou
seja, é do tipo nxn).
A toda matriz
quadrada está associado um número ao qual damos o nome de determinante.
Dentre as
várias aplicações dos determinantes na Matemática, temos:
-
resolução de alguns tipos de sistemas de equações lineares;
-
cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices;
Determinante de
1ª ordem
Dada uma matriz
quadrada de 1ª ordem M=[a11], o seu determinante é o número real a11:
det M =Ia11I = a11
Observação: Representamos o
determinante de uma matriz entre duas barras verticais, que não têm o
significado de módulo.
Por exemplo:
|
|
Determinante de 2ª ordem
Dada a matriz
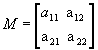 ,
de ordem 2, por definição o determinante associado a M, determinante de
2ª ordem, é dado por:
,
de ordem 2, por definição o determinante associado a M, determinante de
2ª ordem, é dado por: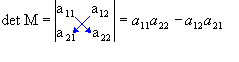
Portanto, o determinante
de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos
da diagonal principal e o produto dos elementos da diagonal secundária. Veja o
exemplo a seguir.
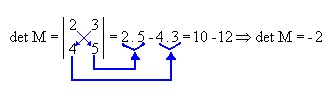
Menor
complementar
Chamamos de menor
complementar relativo a um elemento aij de uma
matriz M, quadrada e de ordem n>1, o determinante MCij ,
de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha
e a coluna que passam por aij .
Vejamos como
determiná-lo pelos exemplos a seguir:
a) Dada a matriz 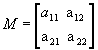 ,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1:
,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1:
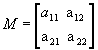 ,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1:
,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1: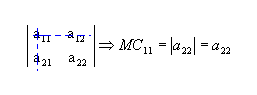
Da mesma forma, o menor complementar relativo
ao elemento a12 é:
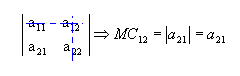
b) Sendo 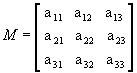 ,
de ordem 3, temos:
,
de ordem 3, temos:
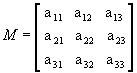 ,
de ordem 3, temos:
,
de ordem 3, temos:Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Veja:
a) Dada
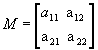 ,
os cofatores relativos aos elementos a11 e a12 da
matriz M são:
,
os cofatores relativos aos elementos a11 e a12 da
matriz M são: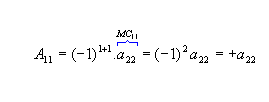 |
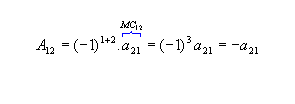 |
b) Sendo 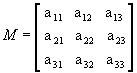 ,
vamos calcular os cofatores A22, A23 e A31:
,
vamos calcular os cofatores A22, A23 e A31:
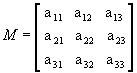 ,
vamos calcular os cofatores A22, A23 e A31:
,
vamos calcular os cofatores A22, A23 e A31: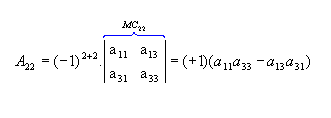 |
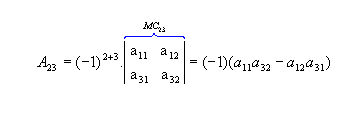 |
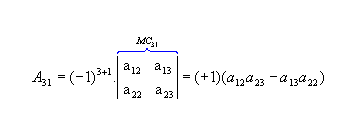 |
Teorema de
Laplace
O determinante
de uma matriz quadrada M = [aij]mxn 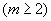 pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (
linha ou coluna) da matriz M pelos respectivos cofatores.
pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (
linha ou coluna) da matriz M pelos respectivos cofatores.
Assim, fixando 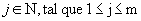 ,
temos:
,
temos:
em que 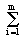 é o somatório de todos os termos de índice i, variando de 1 até m,
é o somatório de todos os termos de índice i, variando de 1 até m,
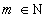 .
.
Regra de Sarrus
O
cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo
prático, denominado regra de Sarrus.
Acompanhe
como aplicamos essa regra para 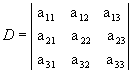 .
.
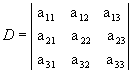 .
.
1º passo: Repetimos
as duas primeiras colunas ao lado da terceira:
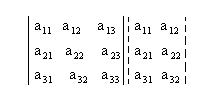
2º passo: Encontramos a soma do
produto dos elementos da diagonal principal com os dois produtos obtidos
pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve
ser precedida do sinal positivo):
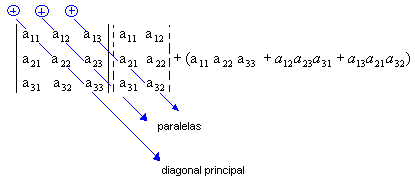
3º passo: Encontramos a soma do
produto dos elementos da diagonal secundária com os dois produtos
obtidos pela multiplicação dos elementos das paralelas a essa diagonal ( a
soma deve ser precedida do sinal negativo):
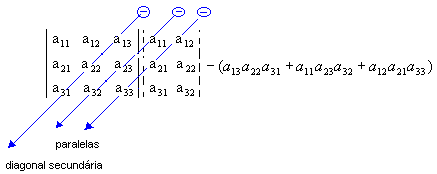
Assim:
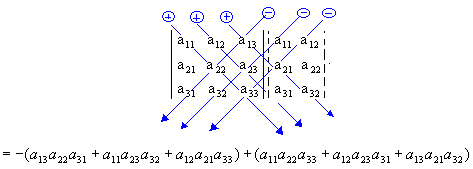
Observação: Se desenvolvermos esse
determinante de 3ª ordem aplicando o Teorema de Laplace, encontraremos o mesmo
número real.
Determinante de
ordem n > 3
Vimos
que a regra de Sarrus é válida para o cálculo do determinante de uma matriz
de ordem 3. Quando a matriz é de ordem superior a 3, devemos empregar o Teorema
de Laplace para chegar a determinantes de ordem 3 e depois aplicar a regra de
Sarrus.
Propriedades dos
determinantes
Os
demais associados a matrizes quadradas de ordem n apresentam as seguintes
propriedades:
P1 ) Quando todos
os elementos de uma fila ( linha ou coluna) são nulos, o determinante dessa
matriz é nulo.
Exemplo:
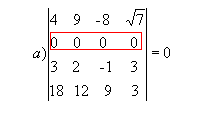 |
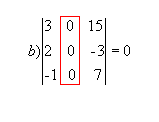 |
P2) Se duas filas de
uma matriz são iguais, então seu determinante é nulo.
Exemplo:
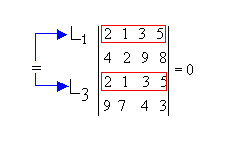
P3) Se duas filas
paralelas de uma matriz são proporcionais, então seu determinante é nulo.
Exemplo:
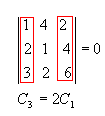
P4) Se os elementos de uma fila de
uma matriz são combinações lineares dos elementos correspondentes de filas
paralelas, então seu determinante é nulo.
Exemplos:
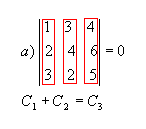 |
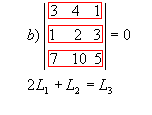 |
P5 ) Teorema de Jacobi: o
determinante de uma matriz não se altera quando somamos aos elementos de uma
fila uma combinação linear dos elementos correspondentes de filas paralelas.
Exemplo:
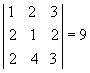
Substituindo a 1ª coluna pela soma dessa
mesma coluna com o dobro da 2ª, temos:
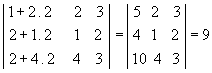
P6) O determinante de uma matriz e
o de sua transposta são iguais.
Exemplo:
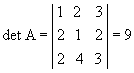 |
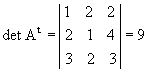 |
Exemplos:
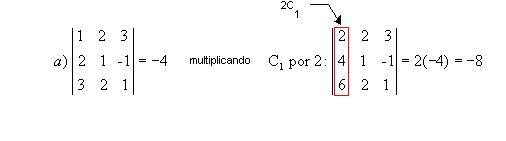 |
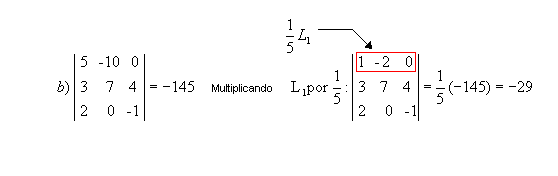 |
Exemplo:
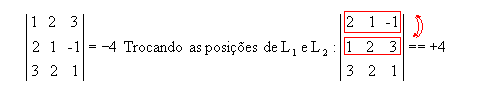
P9) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o determinante é igual ao produto dos elementos dessa diagonal.
Exemplos:
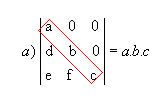 |
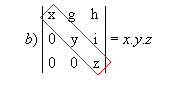 |
Exemplos:
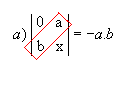 |
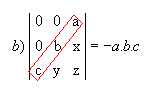 |
P11) Para A e B
matrizes quadradas de mesma ordem n,  .
Como:
.
Como: 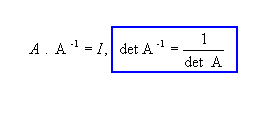
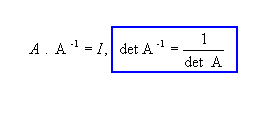
Exemplo:
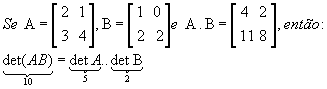
P12) 
Exemplo:
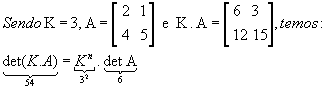
Matrizes
Introdução
O
crescente uso dos computadores tem feito com que a teoria das matrizes seja cada
vez mais aplicada em áreas como Economia, Engenharia, Matemática, Física,
dentre outras. Vejamos um exemplo.
A tabela a
seguir representa as notas de três alunos em uma etapa:
Química
|
Inglês
|
Literatura
|
Espanhol
|
|
A
|
8
|
7
|
9
|
8
|
B
|
6
|
6
|
7
|
6
|
C
|
4
|
8
|
5
|
9
|
Se quisermos saber a nota do
aluno B em Literatura, basta procurar o número que fica na segunda linha
e na terceira coluna da tabela.
Vamos agora considerar uma
tabela de números dispostos em linhas e colunas, como no exemplo acima,
mas colocados entre parênteses ou colchetes:
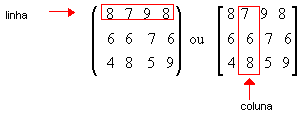
Em tabelas assim
dispostas, os números são os elementos. As linhas são enumeradas de cima
para baixo e as colunas, da esquerda para direita:
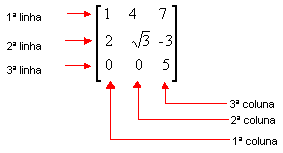
Tabelas com m linhas e n
colunas ( m e n números naturais diferentes de 0) são
denominadas matrizes m x n. Na tabela anterior temos, portanto, uma matriz 3 x
3.
Veja mais alguns exemplos:
-
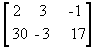 é
uma matriz do tipo 2 x 3
é
uma matriz do tipo 2 x 3 -
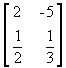 é
uma matriz do tipo 2 x 2
é
uma matriz do tipo 2 x 2
Notação geral
Costuma-se
representar as matrizes por letras maiúsculas e seus elementos por letras
minúsculas, acompanhadas por dois índices que indicam,
respectivamente, a linha e a coluna que o elemento ocupa.
Assim, uma
matriz A do tipo m x n é representada por:

ou, abreviadamente, A = [aij]m
x n, em que i e j representam, respectivamente, a linha e a
coluna que o elemento ocupa. Por exemplo, na matriz anterior, a23
é o elemento da 2ª linha e da 3ª coluna.
Na matriz 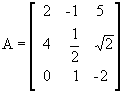 ,
temos:
,
temos:
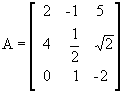 ,
temos:
,
temos: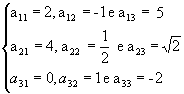
Denominações
especiais
Algumas
matrizes, por suas características, recebem denominações especiais.
-
Matriz linha: matriz do tipo 1 x n, ou seja, com uma única linha. Por exemplo, a matriz A =[4 7 -3 1], do tipo 1 x 4.
-
Matriz coluna: matriz do tipo m x 1, ou seja, com uma única coluna. Por exemplo,
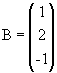 ,
do tipo 3 x 1
,
do tipo 3 x 1
-
Matriz quadrada: matriz do tipo n x n, ou seja, com o mesmo número de linhas e colunas; dizemos que a matriz é de ordem n. Por exemplo, a matriz
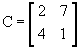 é do tipo 2 x 2, isto é, quadrada de ordem 2.
é do tipo 2 x 2, isto é, quadrada de ordem 2.
Numa matriz
quadrada definimos a diagonal principal e a diagonal secundária. A principal é
formada pelos elementos aij tais que i = j. Na
secundária, temos i + j = n + 1.
Veja:
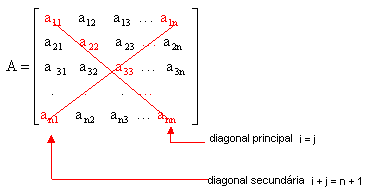
Observe a matriz a seguir:
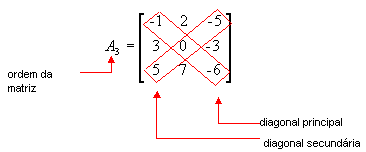
a11 = -1 é elemento da diagonal
principal, pis i = j = 1
a31= 5 é elemento da diagonal
secundária, pois i + j = n + 1 ( 3 + 1 = 3 + 1)
-
Matriz nula: matriz em que todos os elementos são nulos; é representada por 0m x n.
Por exemplo, 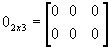 .
.
-
Matriz diagonal: matriz quadrada em que todos os elementos que não estão na diagonal principal são nulos. Por exemplo:
 |
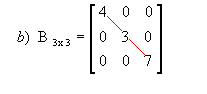 |
-
Matriz identidade: matriz quadrada em que todos os elementos da diagonal principal são iguais a 1 e os demais são nulos; é representada por In, sendo n a ordem da matriz. Por exemplo:
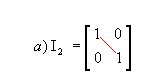 |
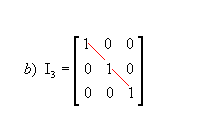 |
Assim, para uma matriz identidade 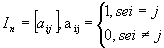 .
.
-
Matriz transposta: matriz At obtida a partir da matriz A trocando-se ordenadamente as linhas por colunas ou as colunas por linhas. Por exemplo:
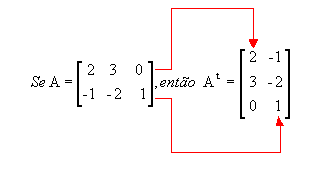
Desse modo, se a matriz A
é do tipo m x n, At é do tipo n x m.
Note que a 1ª linha de A
corresponde à 1ª coluna de At e a 2ª linha de A
corresponde à 2ª coluna de At.
-
Matriz simétrica: matriz quadrada de ordem n tal que A = At . Por exemplo,
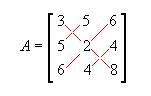 é
simétrica, pois a12 = a21 = 5, a13 = a31
= 6, a23 = a32 = 4, ou seja, temos
sempre a ij = a ij.
é
simétrica, pois a12 = a21 = 5, a13 = a31
= 6, a23 = a32 = 4, ou seja, temos
sempre a ij = a ij.-
Matriz oposta: matriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A. Por exemplo,
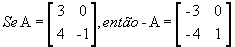 .
.
Igualdade de
matrizes
Duas
matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os
elementos que ocupam a mesma posição são iguais:
Operações
envolvendo matrizes
Adição
Dadas
as matrizes 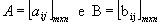 , chamamos
de soma dessas matrizes a matriz
, chamamos
de soma dessas matrizes a matriz 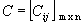 ,
tal que Cij = aij + bij , para todo
,
tal que Cij = aij + bij , para todo 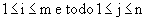 :
:
A + B = C
|
Exemplos:
Observação: A + B existe se, e somente se, A
e B forem do mesmo tipo.
Propriedades
Sendo A, B e C
matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a
adição:
a) comutativa: A + B = B + A
b) associativa: ( A + B) + C = A + ( B + C)
c) elemento neutro: A + 0 = 0 + A = A, sendo
0 a matriz nula m x n
d) elemento oposto: A + ( - A) = (-A) + A = 0
Subtração
Dadas
as matrizes 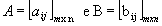 , chamamos
de diferença entre essas matrizes a soma de A com a matriz oposta de B:
, chamamos
de diferença entre essas matrizes a soma de A com a matriz oposta de B:
A - B = A + ( - B )
|
Observe:
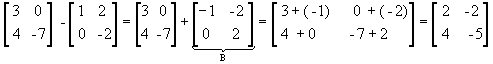
Multiplicação de um número
real por uma matriz
Dados
um número real x e uma matriz A do tipo m x n, o produto de x
por A é uma matriz B do tipo m x n obtida pela multiplicação de
cada elemento de A por x, ou seja, bij = xaij:
B = x.A
|
Observe o seguinte
exemplo:
Propriedades
Sendo
A e B matrizes do mesmo tipo ( m x n) e x e y
números reais quaisquer, valem as seguintes propriedades:
a) associativa: x . (yA) = (xy)
. A
b) distributiva de um número
real em relação à adição de matrizes: x . (A + B) = xA + xB
c) distributiva de uma matriz
em relação à adição de dois números reais: (x + y) . A = xA + yA
d) elemento neutro : xA = A,
para x=1, ou seja, A=A
Multiplicação
de matrizes
O
produto de uma matriz por outra não é determinado por meio do produto dos sus
respectivos elementos.
Assim, o
produto das matrizes A = ( aij) m x p e B = ( bij)
p x n é a matriz C = (cij) m x n em que cada
elemento cij é obtido por meio da soma dos produtos dos
elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima
coluna B.
Vamos
multiplicar a matriz 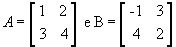 para entender como se obtém cada Cij:
para entender como se obtém cada Cij:
-
1ª linha e 1ª coluna
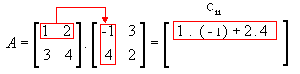
-
1ª linha e 2ª coluna
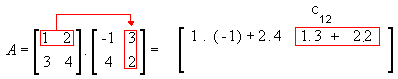
-
2ª linha e 1ª coluna
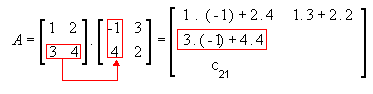
-
2ª linha e 2ª coluna
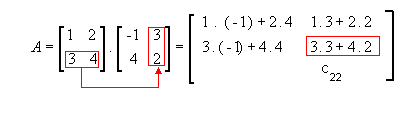
Assim, 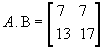 .
.
Observe que:
Portanto, 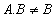 .A,
ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.
.A,
ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.
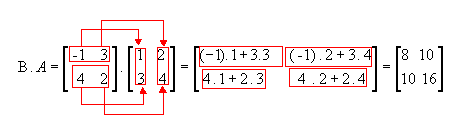
Vejamos outro exemplo com as
matrizes 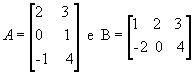 :
:
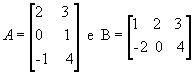 :
: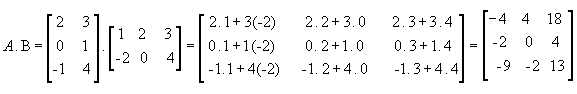
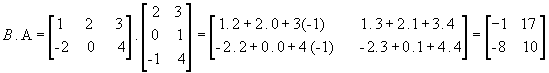
Da definição, temos que
a matriz produto A . B só existe se o número de colunas de A for igual
ao número de linhas de B:
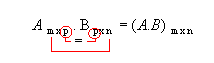
A matriz produto terá o
número de linhas de A (m) e o número de colunas de B(n):
-
Se A3 x 2 e B 2 x 5 , então ( A . B ) 3 x 5
-
Se A 4 x 1 e B 2 x 3, então não existe o produto
-
Se A 4 x 2 e B 2 x 1, então ( A . B ) 4 x 1
Propriedades
Verificadas
as condições de existência para a multiplicação de matrizes, valem as
seguintes propriedades:
a) associativa: ( A . B) . C
= A . ( B . C )
b) distributiva em relação
à adição: A . ( B + C ) = A . B + A . C ou ( A + B ) . C = A . C + B . C
c) elemento neutro: A . In
= In . A = A, sendo In a matriz identidade de
ordem n
Vimos que a
propriedade comutativa, geralmente, não vale para a multiplicação de
matrizes. Não vale também o anulamento do produto, ou seja: sendo 0 m x n
uma matriz nula, A .B =0 m x n não implica, necessariamente, que A =
0 m x n ou B = 0 m x n.
Matriz inversa
Dada
uma matriz A, quadrada, de ordem n, se existir uma matriz A',
de mesma ordem, tal que A . A' = A' . A = In , então A' é
matriz inversa de A . representamos a matriz inversa por A-1
.
fonte: Só matemática
TrigonometriaTrigonometria (do grego trigōnon "triângulo" + metron "medida") é um ramo da matemática que estuda as relações entre os comprimentos de 2 lados de um triângulo retângulo (triângulo onde um dos ângulos mede 90 graus), para diferentes valores de um dos seus ângulos agudos. A abordagem da trigonometria penetra outros campos da geometria, como o estudo de esferas usando a trigonometria esférica.
A trigonometria tem aplicações importantes em vários ramos, tanto como na matemática pura, quanto na matemática aplicada e, consequentemente, nas ciências naturais. A trigonometria é comumente ensinada no Ensino Médio.
Sobre a trigonometria
Dois triângulos são ditos semelhantes se um pode ser obtido pela expansão uniforme do outro. Este é o caso se, e somente se, seus ângulos correspondentes são iguais. O fato crucial sobre triângulos semelhantes é que os comprimentos de seus lados são proporcionais. Isto é, se o maior lado de um triângulo é duas vezes o maior que o lado do triângulo similar, então o menor lado será também duas vezes maior que o menor lado do outro triângulo, e o comprimento do lado médio será duas vezes o valor do lado correspondente do outro triângulo. Assim, a razão do maior lado e menor lado do primeiro triângulo será a mesma razão do maior lado e o menor lado do outro triângulo.Usando estes fatos, definem-se as funções trigonométricas, começando pelos triângulos retângulos (triângulos com um ângulo reto 90 graus ou π/2 radianos). O maior lado em um triângulo qualquer é sempre o lado oposto ao maior ângulo e devido a soma dos ângulos de um triângulo ser 180 graus ou π radianos, o maior ângulo em um triângulo retângulo é o ângulo reto. O maior lado nesse triângulo, consequentemente, é o lado oposto ao ângulo reto, chamado de hipotenusa e os demais lados são chamados de catetos.
Dois triângulos retângulos que compartilham um segundo ângulo
 são necessariamente similares, e a proporção (ou razão) entre o comprimento do lado oposto a
são necessariamente similares, e a proporção (ou razão) entre o comprimento do lado oposto a  e o comprimento da hipotenusa será, portanto, a mesma nos dois triângulos. Este valor será um número entre 0 e 1 que depende apenas de
e o comprimento da hipotenusa será, portanto, a mesma nos dois triângulos. Este valor será um número entre 0 e 1 que depende apenas de  . Este número é chamado de seno de A e é escrito como
. Este número é chamado de seno de A e é escrito como  . Similarmente, pode-se definir :
. Similarmente, pode-se definir :- o cosseno (ou co-seno) de
 : é a proporção do comprimento do cateto adjacente ao ângulo
: é a proporção do comprimento do cateto adjacente ao ângulo  em relação ao comprimento da hipotenusa
em relação ao comprimento da hipotenusa - a tangente trigonométrica de
 : é a proporção do comprimento do cateto oposto ao ângulo
: é a proporção do comprimento do cateto oposto ao ângulo  em relação ao comprimento do cateto adjacente
em relação ao comprimento do cateto adjacente - a co-tangente de
 : é a proporção do comprimento do cateto adjacente ao ângulo
: é a proporção do comprimento do cateto adjacente ao ângulo  em relação ao comprimento do cateto oposto - é o inverso da tangente
em relação ao comprimento do cateto oposto - é o inverso da tangente - a secante trigonométrica de
 : é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto adjacente ao ângulo
: é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto adjacente ao ângulo  - é o inverso do cosseno
- é o inverso do cosseno - a co-secante de
 : é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto oposto ao ângulo
: é a proporção do comprimento da hipotenusa em relação ao comprimento do cateto oposto ao ângulo  - é o inverso do seno.
- é o inverso do seno. Círculo Trigonométrico
Já o Círculo Trigonométrico é um recurso criado para facilitar a visualização destas proporções entre os lados dos triângulos retângulos. Ele consiste em uma circunferência orientada de raio unitário, centrada na origem dos 2 eixos de um plano cartesiano ortogonal, ou seja, um plano definido por duas retas perpendiculares entre si, ambas com o valor 0 (zero) no ponto onde elas se cortam. Existem dois sentidos de marcação dos arcos no ciclo: o sentido positivo, chamado de anti-horário, que se dá a partir da origem dos arcos até o lado terminal do ângulo correspondente ao arco; e o sentido negativo, ou horário, que se dá no sentido contrário ao anterior.
Seno
Dado um triângulo retângulo, o seno de um dos seus 2 ângulos agudos é a proporção entre o comprimento do cateto oposto a este ângulo e o comprimento da hipotenusa, calculada, como toda proporção, pela divisão de um valor pelo outro, a referência da proporção.
No círculo trigonométrico, o seno de um ângulo qualquer pode ser visualizado na projeção do seu raio (por definição igual a 1) sobre o eixo vertical.
Cosseno
No círculo trigonométrico, o cosseno de um ângulo qualquer pode ser visualizado na projeção do seu raio (por definição igual a 1) sobre o eixo horizontal.
Como o cosseno é esta projeção, e o raio do ciclo trigonométrico é igual a 1, segue que, , ou seja, a imagem do cosseno é o intervalo fechado
, ou seja, a imagem do cosseno é o intervalo fechado ![[-1,1]](http://upload.wikimedia.org/wikipedia/pt/math/d/0/6/d060b17b29e0dae91a1cac23ea62281a.png) .
.
Tangente
No círculo trigonométrico, o valor da tangente de um ângulo qualquer pode ser visualizado na reta vertical que tangencia este círculo no ponto em que ele corta o eixo horizontal do lado direito. Nesta reta tangente ao círculo trigonométrico, o valor da tangente trigonométrica de qualquer ângulo é representado pelo segmento que vai do ponto em que ela corta o eixo horizontal até o ponto em que ela corta a reta que contém o raio do círculo trigonométrico para o ângulo considerado. Para avaliar este valor, deve-se compará-lo com o raio do círculo trigonométrico que, por definição, é igual a 1, de preferência quando este raio se encontra sobre a parte superior do eixo ortogonal vertical. Observe que, enquanto o seno e o coseno são sempre menores do que o raio do círculo trigonométrico e, portanto, menores do que 1, a tangente trigonométrica pode ser tanto menor quanto maior do que 1.
Algumas relações
Até então, as funções trigonométricas tem sido definidas por ângulos entre 0 e 90 graus (0 e π/2 radianos) apenas. Usando um círculo unitário, pode-se estendê-los para todos argumentos positivos e negativos (veja função trigonométrica).
Uma vez que as funções seno e cosseno tenham sido tabuladas (ou computadas por uma calculadora), pode-se responder virtualmente todas questões sobre triângulos arbitrários, usando a lei dos senos e a lei dos cossenos. Estas leis podem ser usadas para calcular os ângulos restantes e lados de qualquer triângulo bem como dois lados e um ângulo ou dois ângulos e um lado ou três lados conhecidos.
Alguns matemáticos acreditam que a trigonometria foi originalmente inventada para calcular relógios de sol, um tradicional exercício em antigos livros. Isto é também muito importante para a agrimensura.
Teorema de Pitágoras
O teorema de Pitágoras estabelece que "A soma do quadrado das medidas dos catetos (lados que formam o ângulo de 90°, neste caso a e b) é igual ao quadrado da medida da hipotenusa (lado oposto ao ângulo de 90°, ou c)". Assim: c ² = a ² + b ². Um corolário desse teorema é que se os dois catetos forem de mesmo tamanho, a hipotenusa vale o produto do cateto pela raiz quadrada de 2.
Aplicações da trigonometria
Existem diversas aplicações da trigonometria e das funções trigonométricas. Por exemplo, a técnica da triangulação é usada em astronomia para estimar a distância das estrelas próximas; em geografia para estimar distâncias entre divisas e em sistemas de navegação por satélite. As funções seno e cosseno são fundamentais para a teoria das funções periódicas, as quais descrevem as ondas sonoras e luminosas.
Campos que fazem uso da trigonometria ou funções trigonométricas incluem astronomia (especialmente para localização de posições aparentes de objetos celestes, em qual a trigonometria esférica é essencial) e portanto navegação (nos oceanos, em aviões, e no espaço), teoria musical, acústica, óptica, análise de mercado, eletrônica, teoria da probabilidade, estatística, biologia, equipamentos médicos (por exemplo, Tomografia Computadorizada e Ultrassom), farmácia, química, teoria dos números (e portanto criptologia), sismologia, meteorologia, oceanografia, muitas das ciências físicas, solos (inspeção e geodesia), arquitetura, fonética, economia, engenharia, gráficos computadorizados, cartografia, cristalografia e desenvolvimento de jogos.
Identidades Trigonométricas
Algumas equações envolvendo funções trigonométricas são verdade para todos os ângulos e são conhecidas como "identidades trigonométricas". Muitas expressam relações geométricas importantes. Por exemplo, as identidades Pitagoreanas são uma expressão do Teorema de Pitágoras. Aqui há algumas das identidades mais comumente utilizadas, assim como as fórmulas mais importantes conectando ângulos e lados de um triângulo arbitrário.
Fórmula fundamental da trigonometria e seus corolários
Identidades de soma e subtração
Fórmulas da duplicação do ângulo
Fórmulas da divisão do ângulo em dois
Note que significa que pode haver qualquer dos dois sinais, dependendo do valor de
significa que pode haver qualquer dos dois sinais, dependendo do valor de  .
.
Identidades triangulares
As identidades que se seguem referem-se a um triângulo com ângulos ,
,  e
e  e lados de comprimentos
e lados de comprimentos  ,
,  e
e  , como na figura ao lado. Repare que o lado oposto ao ângulo
, como na figura ao lado. Repare que o lado oposto ao ângulo  é o de comprimento
é o de comprimento  , o lado oposto ao ângulo
, o lado oposto ao ângulo  é o de comprimento
é o de comprimento  e o lado oposto ao ângulo
e o lado oposto ao ângulo  é o de comprimento
é o de comprimento  .
.
Lei dos senos
Lei dos cossenos
- A lei dos cossenos (também conhecida como fórmula dos cossenos) é uma extensão do teorema de Pitágoras para triângulos arbitrários:
Lei das tangentes
A lei das tangentes:
Sendo:
- Sen(A) é comprimento do cateto oposto e
- Cos(A) A o comprimento do cateto adjacente.
fonte: wikipedia

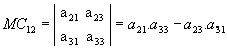




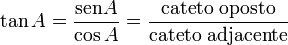
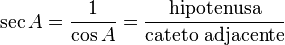












![\frac{a+b}{a-b}=\frac{\tan\left[\tfrac{1}{2}(A+B)\right]}{\tan\left[\tfrac{1}{2}(A-B)\right]}](http://upload.wikimedia.org/wikipedia/pt/math/8/e/c/8ecc3d7514a107662d79d2b6e0678995.png)
![\frac{b+c}{b-c}=\frac{\tan\left[\tfrac{1}{2}(B+C)\right]}{\tan\left[\tfrac{1}{2}(B-C)\right]}](http://upload.wikimedia.org/wikipedia/pt/math/9/c/6/9c64cb1bc9766cc2165e86b15a300790.png)
![\frac{a+c}{a-c}=\frac{\tan\left[\tfrac{1}{2}(A+C)\right]}{\tan\left[\tfrac{1}{2}(A-C)\right]}](http://upload.wikimedia.org/wikipedia/pt/math/7/6/b/76ba3277c7c47646bac125eaab64e9e4.png)
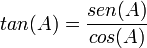
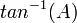

Nenhum comentário:
Postar um comentário