Função
Quadrática
DefiniçãoChama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a
Vejamos alguns exemplos de função quadráticas:
- f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
- f(x) = x2 -1, onde a = 1, b = 0 e c = -1
- f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
- f(x) = - x2 + 8x, onde a = 1, b = 8 e c = 0
- f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a
Exemplo:
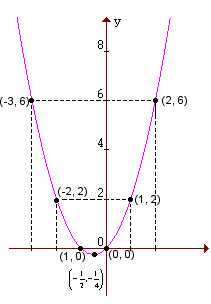
Vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
|
 |
Observação:
Ao construir o
gráfico de uma função quadrática y = ax2 + bx +
c, notaremos
sempre que:
-
se a > 0, a parábola tem a concavidade voltada para cima;
-
se a < 0, a parábola tem a concavidade voltada para baixo;
Zero e Equação do
2º Grau
Chama-se zeros ou
raízes da função polinomial do 2º grau f(x) = ax2 + bx + c ,
a  0,
os números reais x tais que f(x) = 0.
0,
os números reais x tais que f(x) = 0.
Então as raízes da função
f(x) = ax2 + bx + c são as
soluções da equação do 2º grau ax2 + bx + c =
0, as quais são
dadas pela chamada fórmula de Bhaskara:
|
|
Temos:
Observação
A quantidade de
raízes reais de uma função quadrática depende do valor obtido para o
radicando 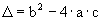 , chamado
discriminante, a saber:
, chamado
discriminante, a saber:
-
quando
 é positivo, há duas raízes reais e distintas;
é positivo, há duas raízes reais e distintas; -
quando
 é zero, há só uma raiz real;
é zero, há só uma raiz real; -
quando
 é negativo, não há raiz real.
é negativo, não há raiz real.
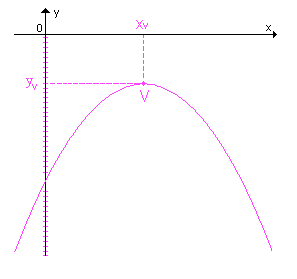
Coordenadas
do vértice da parábola
Quando a >
0, a
parábola tem concavidade voltada para cima e um ponto de mínimo
V; quando a
< 0, a parábola tem concavidade voltada para baixo e um ponto de máximo
V.
Em qualquer caso, as coordenadas de V são 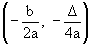 .
Veja os gráficos:
.
Veja os gráficos:
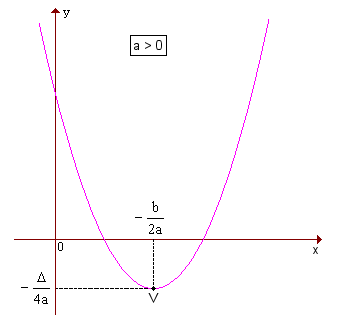
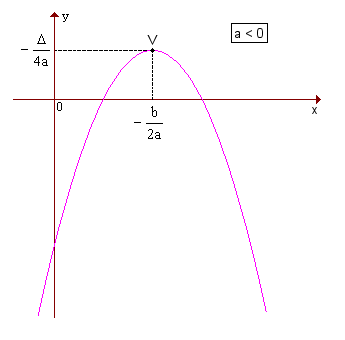
O conjunto-imagem Im da função y = ax2 + bx + c, a
1ª - quando a > 0,
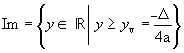
|
a > 0
|
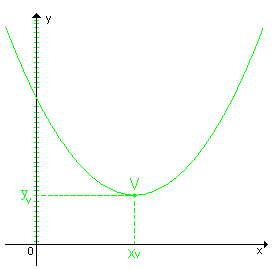
2ª quando a < 0,
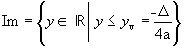
|
a < 0
|
Construção da
Parábola
É
possível construir o gráfico de uma função do 2º grau sem montar a tabela
de pares (x, y), mas seguindo apenas o roteiro de observação seguinte:
-
O valor do coeficiente a define a concavidade da parábola;
-
Os zeros definem os pontos em que a parábola intercepta o eixo dos x;
-
O vértice V
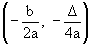 indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
indica o ponto de mínimo (se a > 0), ou máximo (se a< 0); -
A reta que passa por V e é paralela ao eixo dos y é o eixo de simetria da parábola;
-
Para x = 0 , temos y = a · 02 + b · 0 + c = c; então (0, c) é o ponto em que a parábola corta o eixo dos y.
Sinal
Consideramos uma função quadrática y = f(x) = ax2 + bx + c
e
determinemos os valores de x para os quais y é negativo e os valores de x para
os quais y é positivos.
Conforme o sinal do discriminante = b2 - 4ac, podemos ocorrer os seguintes casos:
= b2 - 4ac, podemos ocorrer os seguintes casos:
Conforme o sinal do discriminante
1º -
 > 0
> 0
Nesse caso a função quadrática admite dois zeros reais distintos (x1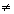 x2). a parábola intercepta o eixo Ox em dois pontos e o sinal da
função é o indicado nos gráficos abaixo:
x2). a parábola intercepta o eixo Ox em dois pontos e o sinal da
função é o indicado nos gráficos abaixo:
Nesse caso a função quadrática admite dois zeros reais distintos (x1
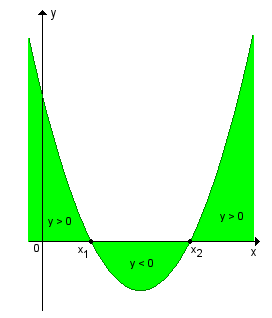
| quando a > 0 |
y > 0  (x
< x1 ou x > x2)
(x
< x1 ou x > x2)
y < 0 x1
< x < x2
x1
< x < x2
y < 0
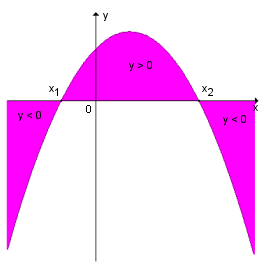
| quando a < 0 |
y > 0  x1
< x < x2
x1
< x < x2
y < 0 (x < x1 ou x > x2)
(x < x1 ou x > x2)
y < 0
2º
-  = 0
= 0
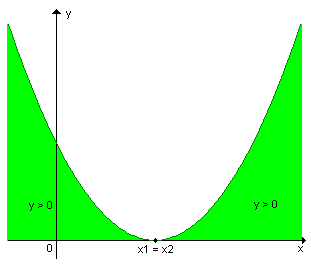
| quando a > 0 |
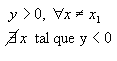
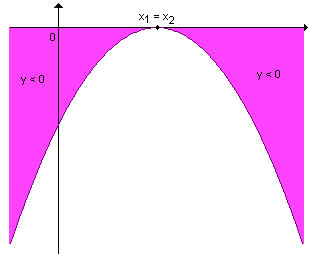
|
quando a <
0
|
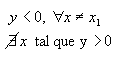
3º
-  < 0
< 0
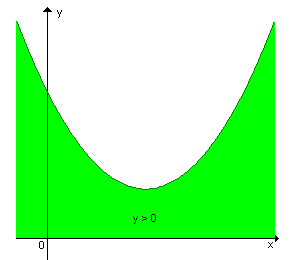
| quando a > 0 |
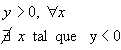
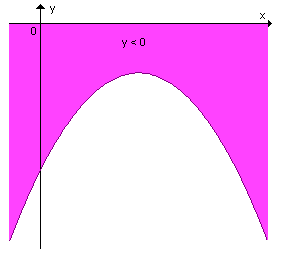
|
quando a <
0
|
Função
de 1º grau
DefiniçãoChama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a
Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
Veja alguns exemplos de funções polinomiais do 1º grau:
f(x) = 5x - 3, onde a = 5 e b = - 3
f(x) = -2x - 7, onde a = -2 e b = - 7
f(x) = 11x, onde a = 11 e b = 0
Gráfico
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a
Exemplo:
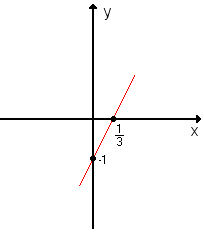
Vamos construir o gráfico da função y = 3x - 1:
Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
a) Para x = 0, temos y = 3 · 0 - 1 = -1; portanto, um ponto é (0, -1).
b) Para y = 0, temos 0 = 3x - 1; portanto,
Marcamos os pontos (0, -1) e
|
 |
Já vimos que o
gráfico da função afim y
= ax + b é uma
reta.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, a está ligado à inclinação da reta em relação ao eixo Ox.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, a está ligado à inclinação da reta em relação ao eixo Ox.
O termo constante,
b, é chamado coeficiente linear da reta.
Para x = 0, temos y
= a · 0 + b = b. Assim, o coeficiente linear é a ordenada do ponto em que a
reta corta o eixo Oy.
Zero e Equação do
1º Grau
Chama-se zero ou raiz
da função polinomial do 1º grau f(x)
= ax + b, a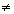 0,
o número real x
tal que f(x)
= 0.
0,
o número real x
tal que f(x)
= 0.
Temos:
f(x) =
0  ax + b =
0
ax + b =
0 
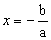
Vejamos alguns
exemplos:
-
Obtenção do zero da função f(x) = 2x - 5:
f(x) = 0 2x - 5 =
0
2x - 5 =
0 
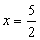
-
Cálculo da raiz da função g(x) = 3x + 6:
g(x) = 0 3x + 6 =
0
3x + 6 =
0  x = -2
x = -2
-
Cálculo da abscissa do ponto em que o gráfico de h(x) = -2x + 10 corta o eixo das abicissas:
O ponto em que o gráfico corta o eixo dos x é aquele em que h(x) = 0; então:
h(x) = 0 -2x + 10 =
0
-2x + 10 =
0  x = 5
x = 5
Crescimento e
decrescimento
Consideremos a
função do 1º grau y = 3x - 1. Vamos atribuir valores cada vez maiores a x e
observar o que ocorre com y:
|
a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
Justificativa:
- para a > 0: se x1 < x2, então ax1 < ax2. Daí, ax1 + b < ax2 + b, de onde vem f(x1) < f(x2).
- para a < 0: se x1 < x2,
então ax1 > ax2. Daí, ax1 + b > ax2
+ b, de onde vem f(x1) > f(x2).Sinal
Estudar o sinal de uma qualquer y = f(x) é determinar os valor de x para os quais y é positivo, os valores de x para os quais y é zero e os valores de x para os quais y é negativo.
Consideremos uma função afim y = f(x) = ax + b vamos estudar seu sinal. Já vimos que essa função se anula pra raiz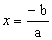 .
Há dois casos possíveis:
.
Há dois casos possíveis:
1º) a > 0 (a função é crescente)y > 0 ax + b > 0
ax + b > 0  x >
x > 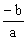 y < 0
y < 0 ax + b < 0
ax + b < 0  x <
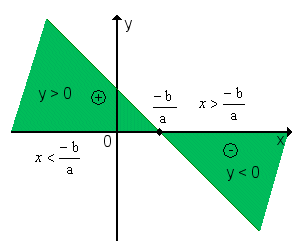
x < 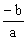 Conclusão: y é positivo para valores de x maiores que a raiz; y é negativo para valores de x menores que a raiz2º) a < 0 (a função é decrescente)
Conclusão: y é positivo para valores de x maiores que a raiz; y é negativo para valores de x menores que a raiz2º) a < 0 (a função é decrescente)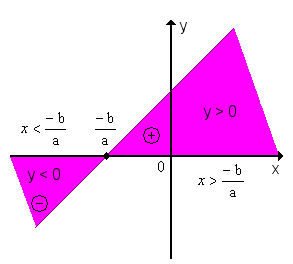
y > 0 ax + b > 0
ax + b > 0  x <
x < 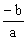
y < 0 ax + b < 0
ax + b < 0  x >
x > 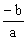
Conclusão: y é positivo para valores de x menores que a raiz; y é negativo para valores de x maiores que a raiz.
fonte: Só Matemática
Conjunto
Na matemática, um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos que compõem o conjunto A, dizemos que x pertence a A .Nos conjuntos, a ordem e a quantidade de vezes que os elementos estão listados na coleção não é relevante. Em contraste, uma coleção de elementos na qual a multiplicidade, mas não a ordem, é relevante, é chamada multiconjunto. Dizemos que dois conjuntos são iguais se e somente se cada elemento de um é também elemento do outro.
Importância
Um conjunto é considerado um dos conceitos mais básicos da matemática, sendo o elemento principal da teoria dos conjuntos.Notação matemática
É possível descrever o mesmo conjunto de três maneiras diferentes, por meio de uma:- lista os seus elementos (ideal para conjuntos pequenos e finitos);
- definição de uma propriedade de seus elementos (o que, se for feito de forma descuidada, pode gerar problemas, tais como o paradoxo de Russell, em Principia Mathematica);
- representação gráfica.
Conceitos essenciais
- Conjunto: representa uma coleção de objetos, geralmente representado por letras maiúsculas;
- Elemento: qualquer um dos componentes de um conjunto, geralmente representado por letras minúsculas;
- Pertinência: é a característica associada a um elemento que faz parte de um conjunto. Se
 é um elemento de
é um elemento de  , podemos dizer que o elemento
, podemos dizer que o elemento  pertence ao conjunto
pertence ao conjunto  e podemos escrever
e podemos escrever  . Se
. Se  não é um elemento de
não é um elemento de  , nós podemos dizer que o elemento
, nós podemos dizer que o elemento  não pertence ao conjunto
não pertence ao conjunto  e podemos escrever
e podemos escrever  .
. Axiomas e propriedades
Os axiomas e propriedades dos conjuntos seguem um contexto metodológico isomórfico à lógica das proposições.
Subconjuntos próprios e impróprios
Se e
e  são conjuntos e todo o elemento
são conjuntos e todo o elemento  pertencente a
pertencente a  também pertence a
também pertence a  , então o conjunto
, então o conjunto  é dito um subconjunto do conjunto
é dito um subconjunto do conjunto  , denotado por
, denotado por  . Note que esta definição inclui o caso em que
. Note que esta definição inclui o caso em que  e
e  possuem os mesmos elementos, isto é, são o mesmo conjunto (
possuem os mesmos elementos, isto é, são o mesmo conjunto ( ). Se
). Se  e ao menos um elemento pertencente a
e ao menos um elemento pertencente a  não pertence a
não pertence a  , então
, então  é chamado de subconjunto próprio de
é chamado de subconjunto próprio de  , denotado por
, denotado por  . Todo conjunto é subconjunto dele mesmo, entretanto não se enquadra na definição de subconjunto próprio, e é chamado de subconjunto impróprio.
. Todo conjunto é subconjunto dele mesmo, entretanto não se enquadra na definição de subconjunto próprio, e é chamado de subconjunto impróprio.



Conjunto vazio
Todo conjunto também possui como subconjunto o conjunto vazio representado por { } ou .
.Podemos mostrar isto supondo que se o conjunto vazio não pertence ao conjunto em questão, então o conjunto vazio deve possuir um elemento ao menos que não pertença a este conjunto. Como o conjunto vazio não possui elementos, isto não é possível. Como todos os conjuntos vazios são iguais uns aos outros, é permissível falar de um único conjunto sem elementos.
Cardinalidade
Mesmo se o conjunto não possui um número finito de elementos, pode-se definir a cardinalidade, graças ao trabalho desenvolvido pelo matemático Georg Cantor. Neste caso, a cardinalidade poderá ser
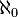 (aleph-0),
(aleph-0), 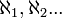 .
.Nos dois casos a cardinalidade de um conjunto
 é denotada por
é denotada por 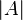 . Se para dois conjuntos A e B é possível fazer uma relação um-a-um entre seus elementos, então
. Se para dois conjuntos A e B é possível fazer uma relação um-a-um entre seus elementos, então  .
.Conjunto potência ou de partes
O conjunto de todos os subconjuntos de um conjunto dado é chamado de conjunto potência (ou conjunto das partes) de
é chamado de conjunto potência (ou conjunto das partes) de  , denotado por
, denotado por  . O conjunto potência é uma álgebra booleana sobre as operações de união e interseção.
. O conjunto potência é uma álgebra booleana sobre as operações de união e interseção.Sendo o conjunto dado A finito, com n elementos, prova-se que o número de subconjuntos ou o número de elementos do conjunto potência ou conjunto das partes de A é
 , ou seja, a cardinalidade do conjunto das partes de A é igual a
, ou seja, a cardinalidade do conjunto das partes de A é igual a  . Como existe uma bijecção entre o conjunto das partes de A e o conjunto
. Como existe uma bijecção entre o conjunto das partes de A e o conjunto  , é usual representar-se P(A) por
, é usual representar-se P(A) por  .
.O Teorema de Cantor estabelece que
 .
.Produto cartesiano
O produto cartesiano de dois conjuntos A e B é o conjunto de pares ordenados: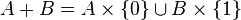 .
.
Função
Função é um dos conceitos mais importantes da matemática. Existem várias definições, dependendo da forma como são escolhidos os axiomas. Uma relação entre dois conjuntos, onde há uma relação entre cada um de seus elementos. Também pode ser uma lei que para cada valor x é correspondido por um elemento y, também denotado por f(x). Existem inúmeros tipos de funções matemáticas, entre as principais temos: função sobrejetora, função injetora, função bijetora, função trigonométrica, Função linear, função modular, função quadrática, função exponencial, função logarítmica, função polinomial, dentre inúmeras outras. Cada função é definida por leis generalizadas e propriedades específicas.
Propriedades da Função Exponencial
- Sendo a > 0 e a ≠ 1, tem-se que ax=at↔ x = t;
- A função exponencial ƒ(x)=ax é crescente em todo seu domínio se, e somente se, a>1;
- A função exponencial ƒ(x)=ax é decrescente em todo seu domínio se, e somente se, 0<a<1;
- Toda função exponencial, isto é, ƒ(x)=ax com a ∈ R+* e a ≠ 1 é bijetora;
A função exponencial é uma das mais importantes funções da matemática. Descrita como ex (onde e é a constante matemática neperiana, base do logarítmo neperiano), pode ser definida de duas maneiras equivalentes: a primeira, como uma série infinita; a segunda, como limite de uma seqüência:
A curva ex jamais toca o eixo x, embora apresente tendência a se aproximar deste.
 corresponde ao fatorial de n e x é qualquer número real ou complexo.
corresponde ao fatorial de n e x é qualquer número real ou complexo.O valor de
 é aproximadamente
é aproximadamente 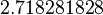
Se x é real, então ex é sempre positivo e crescente. Consequentemente, sua função inversa, o logarítmo neperiano, ln(x), é definida para qualquer valor positivo de x. Usando o logaritmo neperiano, pode-se definir funções exponenciais mais genéricas, como abaixo:
 .
.A função exponencial também gera funções trigonométricas (como pode ser visto na equação de Euler para análises complexas), e as funções hiperbólicas. Então, tem-se que qualquer função elementar, exceto as polinomiais são criadas a partir da função exponencial.
As funções exponenciais "transitam entre a adição e a multiplicação" como é expressado nas seguintes leis exponenciais:

![\sqrt[c]{a}^b = a^{b \over c}](http://upload.wikimedia.org/wikipedia/pt/math/1/8/0/1801240b8ac015e6017d9c725dd99a94.png)
Função exponencial e equações diferenciais
A maior importância das funções exponenciais nos campos das ciências é o fato de que essas funções são múltiplas de suas próprias derivadas:
A função exponencial então resolve a equação diferencial básica
Função exponencial no plano complexo
Quando considerada como uma função definida no plano complexo, a função exponencial retém as importantes propriedades: que pode ser escrita como
que pode ser escrita como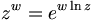 para todos os números complexos z e w.
para todos os números complexos z e w.Isto é também uma função multivalente. As leis exponenciais mencionadas acima permanecem verdade se interpretadas propriamente como afirmações sobre funções multivalentes.
É fácil ver, que a função exponencial descreve qualquer curva no plano complexo a uma espiral logarítmica no plano complexo com centro em 0, nada como o caso de uma reta paralela com os eixos reais ou imaginários descrevem uma curva ou um círculo.
Função exponencial para matrizes e álgebras de Banach
A definição de função exponencial exp dada acima pode ser usada palavra por palavra para cada álgebra de Banach, e em particular para matrizes quadradas. Neste caso temosa (deveríamos adicionar a fórmula geral envolvendo comutadores aqui)
(deveríamos adicionar a fórmula geral envolvendo comutadores aqui)
- ex é invertível com inverso e-x
- a derivada da exp no ponto x é aquela descrição linear que transforma u em u·ex.
 é um elemento fixo da álgebra e
é um elemento fixo da álgebra e  é qualquer número real. Essa função tem importantes propriedades:
é qualquer número real. Essa função tem importantes propriedades:Mapa exponencial nas álgebras de Lie
O "mapa exponencial" que passa uma álgebra de Lie a um grupo de Lie compartilha as propriedades acima, o que explica a terminologia. De fato, desde que R é uma álgebra de Lie de um grupo de Lie de todos os números positivos reais com multiplicação, a função exponencial para argumentos reais é um caso especial da situação da álgebra de Lie. Similarmente, desde que a álgebra de Lie M (n, R) de todas as matrizes reais quadradas pertence ao grupo de Lie de todas as matrizes quadradas invertíveis, a função para matrizes quadradas é um caso especial do mapa exponencial da álgebra de Lie.
fonte: wikipedia




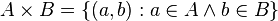



















Nenhum comentário:
Postar um comentário